Mengchang Wang
IIB-LPO: Latent Policy Optimization via Iterative Information Bottleneck
Jan 09, 2026Abstract:Recent advances in Reinforcement Learning with Verifiable Rewards (RLVR) for Large Language Model (LLM) reasoning have been hindered by a persistent challenge: exploration collapse. The semantic homogeneity of random rollouts often traps models in narrow, over-optimized behaviors. While existing methods leverage policy entropy to encourage exploration, they face inherent limitations. Global entropy regularization is susceptible to reward hacking, which can induce meaningless verbosity, whereas local token-selective updates struggle with the strong inductive bias of pre-trained models. To address this, we propose Latent Policy Optimization via Iterative Information Bottleneck (IIB-LPO), a novel approach that shifts exploration from statistical perturbation of token distributions to topological branching of reasoning trajectories. IIB-LPO triggers latent branching at high-entropy states to diversify reasoning paths and employs the Information Bottleneck principle both as a trajectory filter and a self-reward mechanism, ensuring concise and informative exploration. Empirical results across four mathematical reasoning benchmarks demonstrate that IIB-LPO achieves state-of-the-art performance, surpassing prior methods by margins of up to 5.3% in accuracy and 7.4% in diversity metrics.
CobBO: Coordinate Backoff Bayesian Optimization
Feb 16, 2021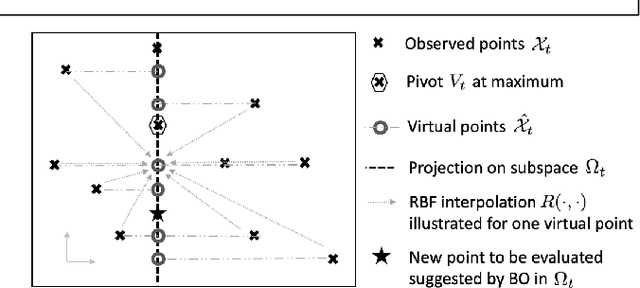

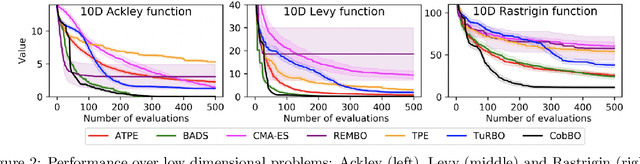

Abstract:Bayesian optimization is a popular method for optimizing expensive black-box functions. The objective functions of hard real world problems are oftentimes characterized by a fluctuated landscape of many local optima. Bayesian optimization risks in over-exploiting such traps, remaining with insufficient query budget for exploring the global landscape. We introduce Coordinate Backoff Bayesian Optimization (CobBO) to alleviate those challenges. CobBO captures a smooth approximation of the global landscape by interpolating the values of queried points projected to randomly selected promising subspaces. Thus also a smaller query budget is required for the Gaussian process regressions applied over the lower dimensional subspaces. This approach can be viewed as a variant of coordinate ascent, tailored for Bayesian optimization, using a stopping rule for backing off from a certain subspace and switching to another coordinate subset. Extensive evaluations show that CobBO finds solutions comparable to or better than other state-of-the-art methods for dimensions ranging from tens to hundreds, while reducing the trial complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge